Frequency graph cumulative draw
Table of Contents
Table of Contents
If you are studying statistics or mathematics, then you must have heard about cumulative frequency graphs. These graphs are used to represent data in a way that is easy to understand and analyze. Drawing cumulative frequency graphs can be a challenging task, but with the right guidance, you can do it with ease.
Many students struggle with the concept of how to draw cumulative frequency graphs, which can result in frustration and loss of time. Understanding the concepts and techniques behind drawing cumulative frequency graphs is essential to analyze data and make informed decisions.
Before we delve into how to draw cumulative frequency graphs, let’s first understand what it represents. A cumulative frequency graph is a representation of how many times a particular value or a range of values appears in a given dataset. These graphs are used to show the distribution of data and help make sense of large data sets.
To draw a cumulative frequency graph, you need to follow a few simple steps. First, organize your data in ascending order, such that the smallest value appears first. Next, create a tally chart, and count how many times each value appears. Finally, plot the cumulative frequency for each value or range of values.
My Experience with Drawing Cumulative Frequency Graphs
When I was first introduced to the concept of cumulative frequency graphs, I found it incredibly confusing. However, with time and practice, I have become proficient at drawing them. When teaching others how to draw cumulative frequency graphs, I find it helpful to break down the process into simple steps and provide examples to guide them.
Important Considerations when Drawing Cumulative Frequency Graphs
When drawing cumulative frequency graphs, it is essential to keep in mind the following:
- The data should be accurate and relevant to the research question
- Labels and scales should be clear and easy to read
- The graph should be neat and well-presented
- Make sure to choose the correct graph type based on the data
The Importance of Accurate Data in Cumulative Frequency Graphs
Accurate data is crucial when drawing cumulative frequency graphs. Invalid or incorrect data can produce unreliable or misleading results. Therefore, always ensure that the data you use is relevant to the research question and accurate. You can use software or programs to help with data analysis and reduce the risk of errors.
Choosing the Right Graph Type for Your Data
The choice of the graph type for your data is equally important. A wrong choice of graph can produce misleading results or misinterpretations of data. Common types of graphs used are line graphs, bar graphs, and pie charts. When choosing which graph type to use, consider the data type, the extent of the data, and the audience.
Question and Answer
Q1. How do you interpret cumulative frequency graphs?
A cumulative frequency graph represents the distribution of data in a given data set. The x-axis represents the data, and the y-axis represents the cumulative frequency. The graph can provide insights into trends, modes, medians, and means of the data. Essentially, it helps you analyze data and make informed decisions.
Q2. Can you draw cumulative frequency graphs from qualitative data?
Cumulative frequency graphs can be drawn from both qualitative and quantitative data. Quantitative data is numerical data, while qualitative data is non-numerical data. For qualitative data, you can create groups, tag them, and use the tagging information to draw the cumulative frequency graph.
Q3. What are the different types of cumulative frequency graphs?
There are three types of cumulative frequency graphs: less than, greater than, and cumulative frequency polygon. The less than graph shows the number of values that are less than or equal to a particular value. The greater than graph shows the number of values that are greater than or equal to a particular value. The cumulative frequency polygon is a combination of both less than and greater than graphs.
Q4. How can you spot outliers in cumulative frequency graphs?
Outliers are data points that are significantly different from other data points. These are shown as isolated points or regions of the cumulative frequency graph. Outliers can be spotted by looking at the extremes of the distribution. They can also show up as points far away from the line of best fit.
Conclusion of How to Draw Cumulative Frequency Graphs
In conclusion, drawing cumulative frequency graphs is a crucial part of data analysis in statistics and mathematics. It represents data in an understandable manner, making it easier to analyze and interpret. By following these simple steps, you can easily create an accurate and effective cumulative frequency graph. Remember to always consider the data type, the extent of the data, and the audience when choosing the graph type. Accuracy is critical, so ensure your data is relevant to the question at hand.
Gallery
How To Calculate Cumulative Frequency: 11 Steps (with Pictures)

Photo Credit by: bing.com / frequency cumulative calculate example data step half value wikihow
Cumulative Frequency GCSE Maths Higher Revision Exam Paper Practice
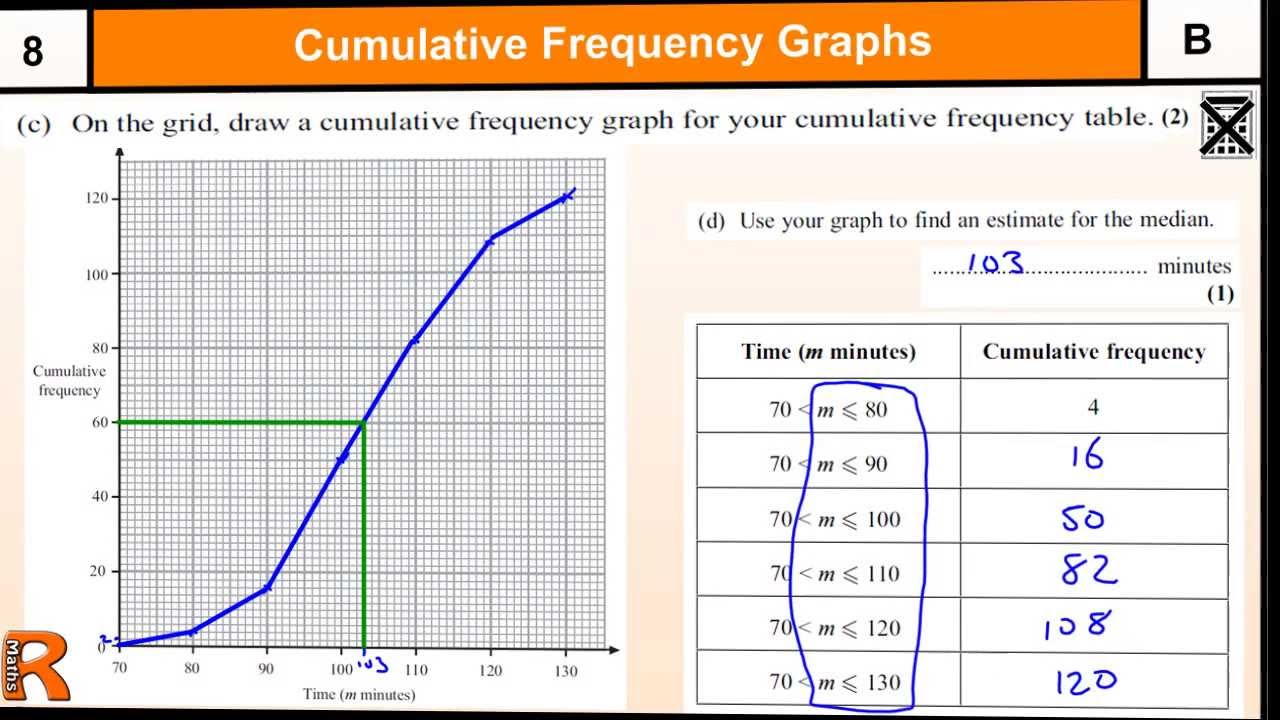
Photo Credit by: bing.com / frequency cumulative gcse maths exam paper practice help higher revision
Interpreting Cumulative Frequency Graphs - Mr-Mathematics.com

Photo Credit by: bing.com / cumulative graphs interpreting
How To Draw A Cumulative Frequency Graph - YouTube
Photo Credit by: bing.com / frequency graph cumulative draw
Maths Forever
Photo Credit by: bing.com / frequency cumulative quartile bitesize median interquartile range quartiles rhwng





